Section: Application Domains
Plasma Physics and fusion energy
Taking into account spatial effects and time evolution of hot plasmas therefore leads to severe numerical challenges first on modeling aspects and second on purely numerical issues like oscillations and multiscale phenomena. Time scales are very different, ranging from pico-seconds to seconds. This requires special treatment to avoid excessive computing time, as for instance slow/fast manifold decomposition or time averaging. These two difficulties lead to the study and development of new robust numerical schemes and algorithms in order to preserve accuracy and stability within reasonable computing time. To speed up model development the use of refined numerical schemes must be as automatized as possible. Slow/fast manifold should be constructed automatically from the model, and spatial discretization should be as transparent as possible in order to apply former works (semi-Lagrangian or particle methods for transport, spectral or finite difference methods for collisions) on this topic.
Our program can be split into three different tasks :
-
derivation of new collision operators based both on Coulombian interactions and strong external forces, approximation of collisional operators for multi-species by developing fast algorithms ;
-
numerical treatment of multi-scale problems applying AP schemes to problems taking into account electromagnetic effects and collisions ;
-
hybrid methods to take advantage of different regimes and reduce the computational cost.
Approximation of collision operators in plasma physics & conception of softwares for collisional plasmas.
An important step in the understanding of high temperature and dense plasmas is to investigate the effect of weakly Coulombian interactions, namely the Landau or Landau-Fokker-Planck collision operator. Due to the high temperature, collisions between particles have been neglected most of the time, but for the long time simulations, it seems that collisions may contribute and induce some nonlinear effects stabilizing the plasma. Furthermore, for inertial and magnetic confinement fusion, classical collision operators are no longer valid since their derivation, based on microscopic interactions only take into account self-interactions but no external forces, which are not negligible in our applications. There are only few works of physicists on this topic in 80's.
Then, our objective is to derive such operators to describe collisional plasmas and to simulate the transport of classical, as well as relativistic electrons, within a multi-species plasma, containing mobile electrons and ions. Issues to be addressed on this topic involve the derivation of multi-scale models due to different scales of effective constants, spatial heterogeneity and strength of boundary conditions.
Moreover, because of the quadratic aspect of the kernel and the multiple integrations in its analytical formulation, the Landau-Fokker-Planck equation is complicated to compute even if fast algorithm are available O(
Collisional plasma and fluid models One characteristic of plasma physics problems is that they involve many different phenomena (instabilities, saturation phenomena due to nonlinear effects which couple different modes), many different time (plasma frequency, girokinetic frequency, etc) and space scales. Splitting a model in sub-models and studying their interactions is a central point, leading to new questions: how to define sub-models? How to simplify or complexify them?
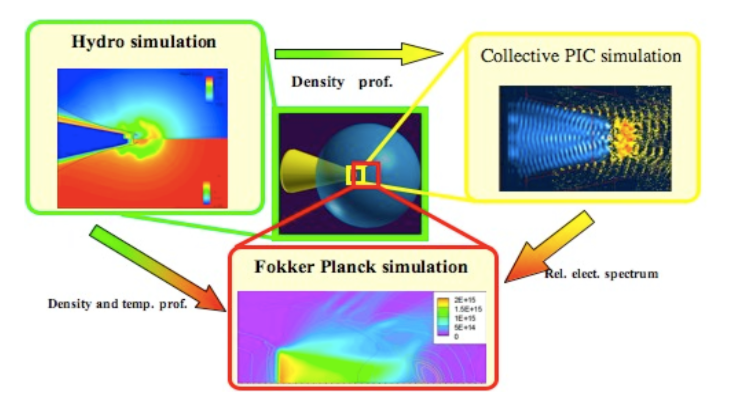
For instance, the interaction of intense lasers with solid matter generates a hot plasma state that is well described by the Vlasov-Maxwell equation at the ignition point, whereas collective effects (electromagnetic fields) and collisions have to be taken into account around the impact and fluid models are sufficient in the capsule (see Figure 1 ). Accurate and efficient modeling of the physics in these scenarios is highly pertinent, because it relates to experimental campaigns to produce energy by inertial confinement fusion on facilities such as the Laser Méga-Joules in Bordeaux. Calculations involving the Vlasov-Fokker-Planck equation are computationally intensive, but are crucial to proper understanding of a wide variety of physical effects and instabilities in inertial fusion plasmas.
|
One of the main challenges from the numerical point of view is to propose a general methodology to design macroscopic fluid models that take into account localized kinetic up-scaling effects (which represents the meso-scale). One approach will consist in considering fluid models, which are solved in the whole domain together with a localized kinetic upscaling that corrects the fluid model wherever it is necessary (non-equilibrium events occurring in the flow). This upscaling is obtained by solving a kinetic equation on the non-equilibrium part of the distribution function. This equation is solved only locally and is related to the fluid equation through a downscaling effect. We want to demonstrate that this approach applies to problems that have a hydrodynamic time scale as well as to problems with diffusion time scale.
The project will therefore combine physical modeling and mathematical analysis in order to achieve an understanding and propose a model of the plasma behavior over the various scales involved. The milestones involved in this project are therefore:
-
set up a new phenomenology allowing to describe non-local effects in any geometry, and based on a state-of-the-art of mathematical modeling of hot plasmas;
-
set up a multiscale model of the physical mechanisms at play at the different scales (micro, meso and macro scales), with a crucial emphasis on the connections between the scales ;
-
propose a mathematical analysis and numerical development of the models, and provide systematic derivations of the connections between the scales.
This program therefore organizes naturally over the various scales at play in the problem and their connections: macroscale phenomenology ; kinetic at mesoscales ; statistical behavior at microscales.